誰もが一度は聞いたことがある「ロジカルシンキング」ですが、「ロジカルシンキングとは一体何なのか」「それは自分の仕事に役立つのか」をわかっていないという人は意外に多いもの。
そんなあなたのために、今さら聞けないロジカルシンキングの超基本スキルを解説します。
ロジカルシンキングの基本だけでもマスターすれば、勘・経験・度胸(いわゆるKKD)に頼っていたあなたの仕事の生産性は劇的に向上し、未経験の問題にも対処できるようになります。
ロジカルシンキング(論理思考)とは

ロジカルシンキング(論理思考)とは、筋道を立てて考える思考の技術です。
正しい認識や判断をするための思考の進め方を研究する論理学をベースに、経営コンサルタントたちが仕事の中で培ってきた技法から生まれました。
ロジカルシンキングは、その土台となるMECEという考え方や、思考の筋道を立てる手法、論理的に思考を広げるためのツールが体系化されています。
ロジカルシンキングをマスターすることで、矛盾がなく誰しもが納得できるような一貫したストーリーを考えたり、説明したりできるようになります。
仕事に役立つロジカルシンキング

ロジカルシンキングは、私たちの仕事のあらゆる場面で役に立つ思考法です。
ロジカルシンキングを仕事で活用すれば次の6つが劇的に向上します。
課題を見つける力
私たちは、日々課題を探しています。
お客様が困っている課題は何か、仕事の効率を上げるための課題は何かなどの課題を見つけて解決することが私たちの仕事の全てです。
適切にお客様の課題を提起できなければお客様の困りごとを解決できず、売り上げや成果につながりません。
そのため、私たちの仕事では適切な課題を提起することが特に重要です。
ロジカルシンキングを学ぶことで、適切な課題を見つける力が向上します。
問題の分析力
私たちは、仕事の中で多くの問題を分析しています。
ロジカルシンキングを使うことで、筋道を立てて問題を整理できるようになり、問題を客観的に分析できるようになります。
また、分析力が向上することで、スムーズに問題の原因を特定できるようになります。
問題解決力
問題の分析だけでなく、解決するための施策を検討する場面でもロジカルシンキングが役に立ちます。
ロジカルシンキングにより、問題の原因を起点とし解決に至るまでのストーリーを矛盾無く立てられるようになるため、問題解決のための的確な施策を立案できるようになります。
プレゼン力・提案力
ロジカルシンキングは思考だけでなく、プレゼンや提案など誰かに自分の考えを話す際にも役に立ちます。
ロジカルシンキングでプレゼンのストーリーを作ることで、誰もが納得できる理屈に合ったストーリーを展開できるようになります。
そのため、プレゼンの説得力が増して、提案が受け入れられやすくなります。
コミュニケーション力
日々の、コミュニケーションでもロジカルシンキングは有効です。
上司や同僚、お客様や取引先と話をするときに、相手が理解しやすいよう筋道をたてた話ができるようになります。
また、相手の話を聞く際にもロジカルシンキングを使って話を整理することで、話の内容を理解しやすくなります。
生産性
ロジカルシンキングで、課題を見つける力、問題解決力、プレゼン・提案力、コミュニケーション力が向上することにより、あなたの仕事のスピードが劇的に高まります。
そのため、これまでより短い時間で高い成果を出せるようになります。
ロジカルシンキングの基本スキル

ロジカルシンキングの基本スキルには大別すると以下の3種類があります。
論理を支える基本の考え方:MECE
MECEとは、Mutually Exclusive and Collectively Exhaustiveの頭文字を取った言葉であり、ミーシー(もしくはミッシー)と読みます。
日本語で、「モレ(漏れ)なく、ダブりなく」と言う意味です。
ロジカルシンキングで物事を考えるとき、モレなくダブりなく考えることが最も重要です。
いくつか例を挙げて考えてみましょう。
ダブりはないがモレがある
例えば、あるセールスパーソンが商品をお客様に売るための販売方法を検討するとします。
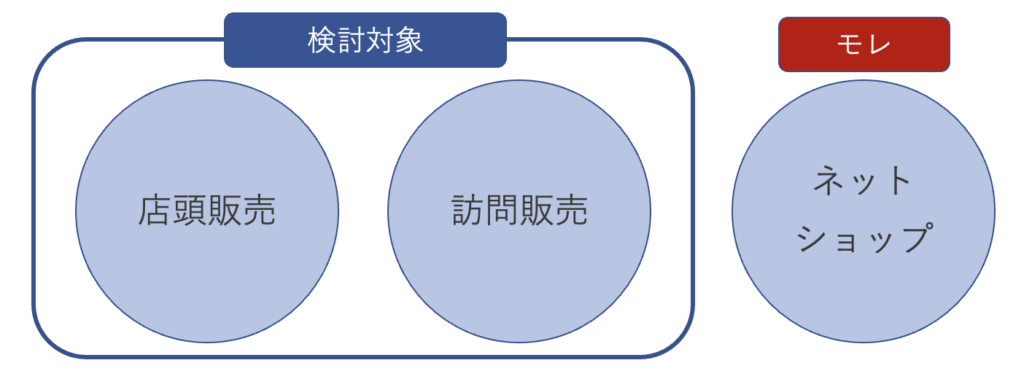
通常、商品を売る方法としては店頭販売やネットショップ、訪問販売などがあります。
ですが、このセールスパーソンが店頭販売と訪問販売のみ検討しネットショップについては未検討だったとしたらどうでしょう。
ネットショップという大きな販売機会を逃してしまい、本来なら出せるはずの成果を出せない可能性があり、セールスパーソンとしては失格です。
モレはないがダブりがある
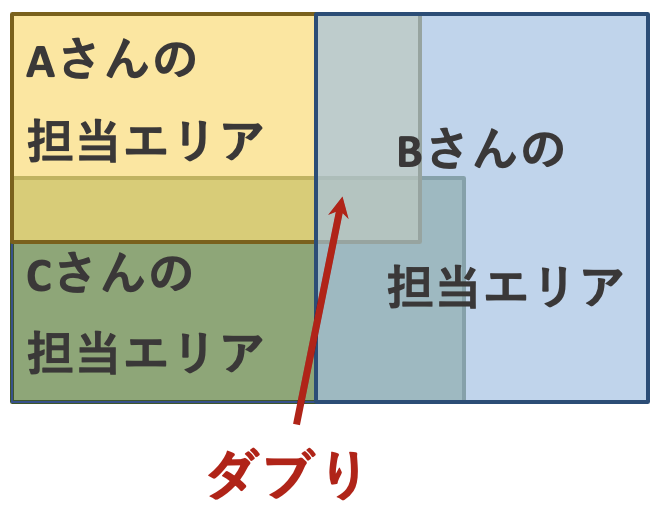
ある会社がセールスパーソンの外回りのエリア分けを検討したとします。
このとき、もしセールスパーソンの担当エリアに重複した箇所があると、同じエリアに複数人のセールスパーソンが足を運ぶことになり、効率のよい営業活動ができません。
効率がよい営業活動を行うには、外回りのエリアがダブらず、担当範囲が明確に分かれていなくてはなりません。
モレもダブりもある
例えば、顧客満足度アンケートをとるために、次の選択肢を顧客に選んでもらうアンケートを作成したとしたらどうなるでしょうか。(現実にはこんなアンケートを作る人はいないと思いますが・・・)

このアンケートでは「接客は満足」が二つもあり、お客様はどちらを選べば良いか迷ってしまいます。
また、商品に満足している人が選択する項目がモレています。
こんなアンケートでは正確な顧客満足度を測ることはできません。
モレがなくダブりもない
コンビニでの商品の陳列を考えてみましょう。
コンビニでは食品・飲料品から日用品や書籍までさまざまな商品を扱っていますが、それぞれの商品を陳列する棚は1つに決まっています。
同じ商品が複数の棚にダブって陳列されていることはありません。
また、飲料水の陳列棚を設置し忘れている(モレている)コンビニはありません。
モレなくダブりなく商品を陳列することで、お客様は自分の目当ての商品を効率よく探し出し購入できます。

このように、ロジカルシンキングで物事を分析したり検討したりするときは、MECEでモレがなくダブりもないように思考することが最も重要です。
そして、このMECEがロジカルシンキングのさまざまな手法やツールを使う際の最も基本的な考え方でもあります。
論理を構築する手法:帰納法と演澤法
私たちが誰かに何かを説明するとき、自然に「よって」「したがって」「このように」と言った言葉を使って話を展開しています。
その際に「よって」「したがって」「このように」の前後の話がつながっていないと、聞いている相手は「話が飛んだ」「筋が通っていない」と感じ、話を理解できません。
例えば次のような説明は、「よって」の前後の話に筋が通ったつながりがありません。
先月はジャンルIの商品AとBの売り上げが大きく落ち込みました。
よって、今月はジャンルIIの商品Dの広告に力を入れるべきです
この説明では、商品A、Bの売り上げが落ちた原因や、商品Dの広告に力を入れる理由の説明が抜けており、「よって」で話がつながっていません。
このような話を展開してしまうと、聞き手に話を遮られて終わるか、聞き手も話の飛びに気付かずに根拠のない商品Bの広告の話題に進んでしまうかのどちらかになってしまいます。
ロジカルシンキングでは、このような話の飛びを防ぎ、道筋を立ててストーリーを構成する手法として、帰納法と演澤法という2つの手法を使います。
帰納法
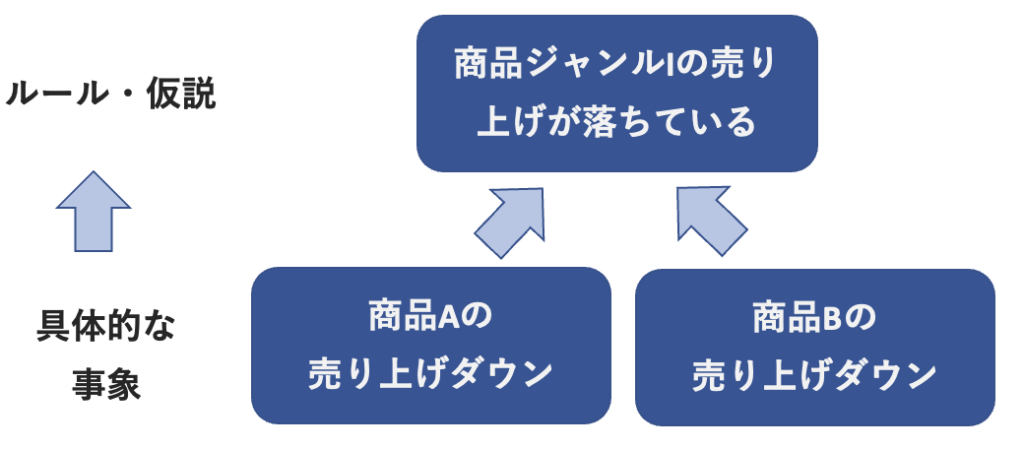
個別的、具体的な事象から、抽象的・普遍的なルールを見いだす推論手法です。
例えば、商品Aの売り上げが落ちている、商品Bの売り上げも落ちているという具体的なデータから、商品ジャンルI全体が売れなくなってきているという、一段上位のルールを推理するのが帰納法です。
ビジネスの現場におけるさまざまな問題を発見したり仮説を立てたりする上で、帰納法は基本的かつ重要な手法です。
ビジネスでは、個別のデータだけでは有効な戦略を立てられません。個別のデータから一段上のルールを推理することで初めて先を見越した有効な戦略が立てられるようになるのです。
例でいうと、商品AとBの売り上げデータだけをみて、A・Bの売り上げを回復させる対策を考えようとしてもうまくいきません。商品ジャンルI全体の売り上げが下がってくるというところに気づけて、初めて別の商品ジャンルで売り上げをカバーするなどの有効な対策が立てられるようになるのです。
例の説明を、帰納法をつかってわかりやすく説明すると次のようになります。
先月はジャンルIの商品AとBの売り上げが大きく落ち込みました。(具体的な事象)
このことから、商品ジャンルI全体が売れなくなってきていることが推測されます。(帰納法による仮説)
そのため、商品A、Bの売り上げをカバーするには別ジャンルの売り上げを上げる必要があります。(有効な戦略)
商品ジャンルIの売り上げダウンをカバーできる商品は、商品ジャンルIIの商品Dしかありません。(MECEで検討)
よって今月はジャンルIIの商品Dの広告に力を入れるべきです。(具体的な打ち手)
演澤法
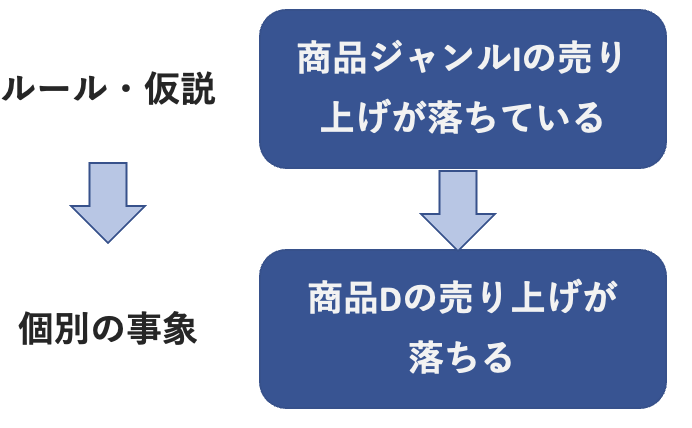
演澤法は、帰納法とは逆に抽象的なルールから個別の事象を導き出す推論手法です。(演澤は「えんたく」と読みます)
よく使われる三段論法は演澤法の一種です。
例えば、次のような説明は演澤法を使った説明です。
「商品ジャンルIの商品は、売り上げが落ちてきています」
「商品CはジャンルIの商品です」
「そのため商品Cの売り上げも落ちてくることが予想されます」
演澤法では、前提となるルールが正しければ、そこから導き出される個別の事象も正しくなります。
論理を整理し可視化するツール:ロジックツリーとピラミッドストラクチャー
ロジカルシンキングを実際に使って物事を分析する際によく使われるツールに、ロジックツリーとピラミッドストラクチャーの2つがあります。
ロジックツリーやピラミッドストラクチャーを駆使して思考を可視化することで、MECEで考えやすくなり、筋道が通った問題解決や提案ができるようになります。
ロジックツリー
ロジックツリーとは、問題の原因や解決策をMECEの考え方を用いてツリー状に分解し、視覚的に整理する問題解決ツールです。
限られた時間の中で問題を整理して原因を追及したり、より良い解決策を導き出したりするのに力を発揮します。
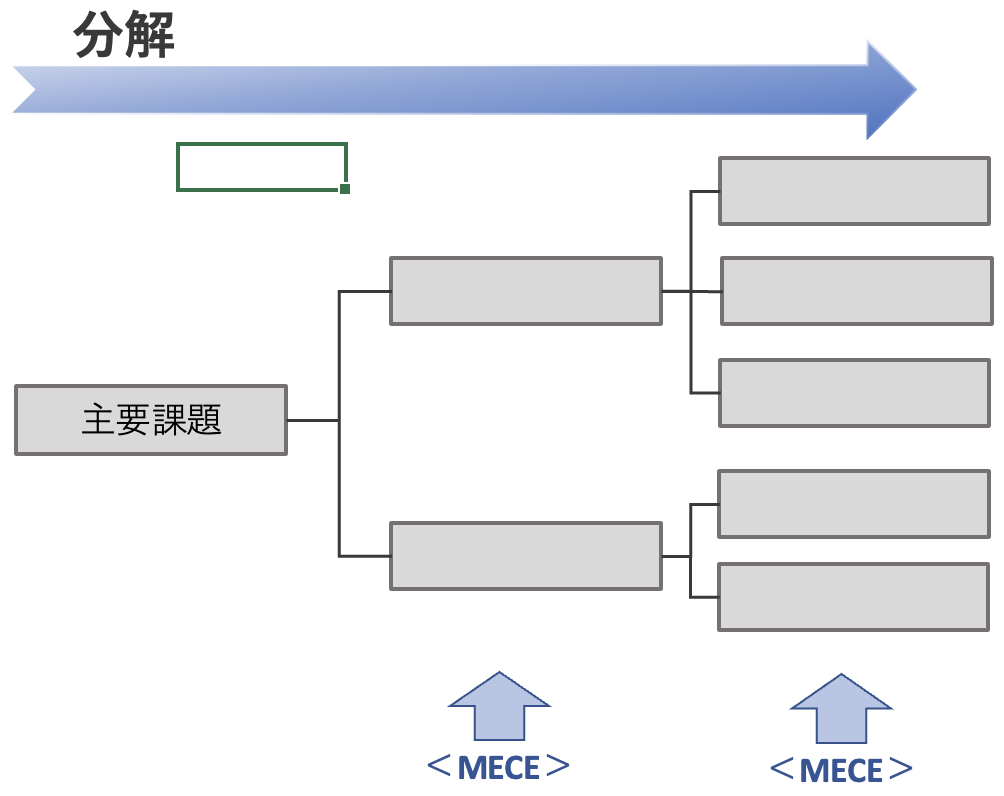
ロジックツリーを使う際の重要なポイントは次の2点です。
- MECEになるよう分解する
- 適切な切り口で分解する
- MECEになるよう分解する
MECEを気にせずに思いつきで枝葉を伸ばすのでは、マインドマップと変わりません。
マインドマップは発想を広げるのには役に立ちますが、ロジックツリーで体系的に問題を整理・分析する際にはMECEであることが重要です。
- 適切な切り口で分解する
問題を分解する切り口は無数にありますが、重要なのは適切な切り口で分解することです。
そのためには、適切な切り口を見つけなければなりません。
そこで、ロジックツリーで問題を分解し整理するときは、まず仮説を立ててその仮説を検証できる切り口で分解します。
3種類のロジックツリー
ロジックツリーは、情報を分解、整理する目的に応じて次の3つの種類に分けられます。
- Whatツリー
- Whyツリー
- Howツリー
- Whatツリー
Whatツリーは、ある物事をその構成要素で分解するロジックツリーです。
親要素(左側)が「何」で構成されているかが子要素(右側)になります。
Whatツリーで物事の構成要素を網羅的に洗い出すことで、問題がどこにあるのかを発見するのに役立ちます。
例えば、今期の売り上げが予算に対して赤字になったという問題があるとき、会社の売り上げを構成する要素を分解して可視化し、構成要素を一つひとつチェックすることで、赤字の原因がどこにあるかを発見できます。
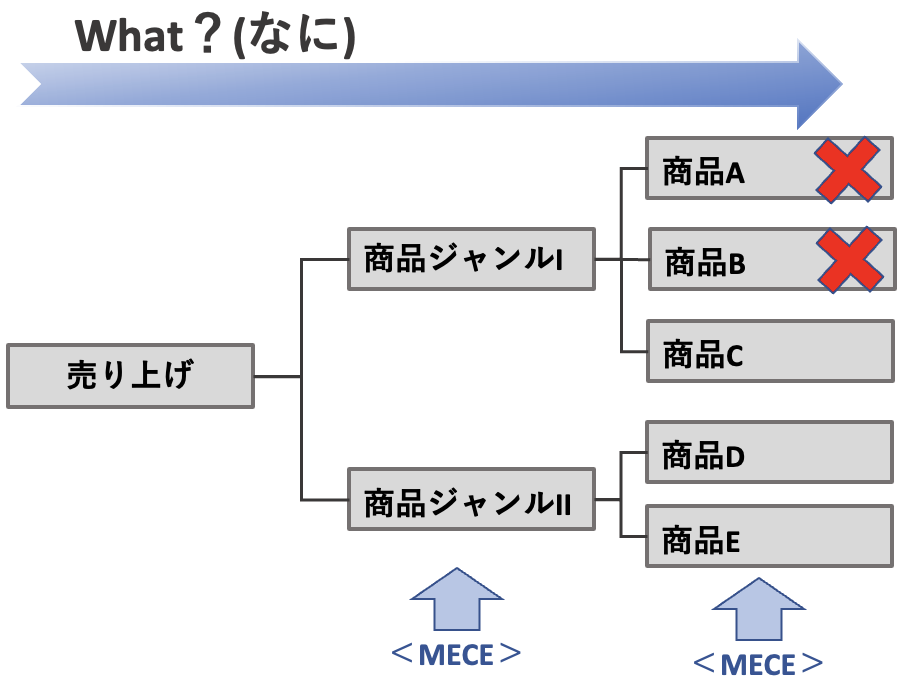
- Whyツリー
Whyツリーは、問題をその原因で分解するロジックツリーです。
親要素(左側)の問題がなぜ発生しているか、その原因が子要素(右側)です。
Whyツリーは問題の原因を深く追及することでその問題の真因を発見するのに役立ちます。
トヨタ発祥の「なぜなぜ分析」は、Whyツリーの一種です。
例えば、商品ジャンルIの売り上げが落ちているという問題の原因を追及することで、その真因が何かを突き止められます。
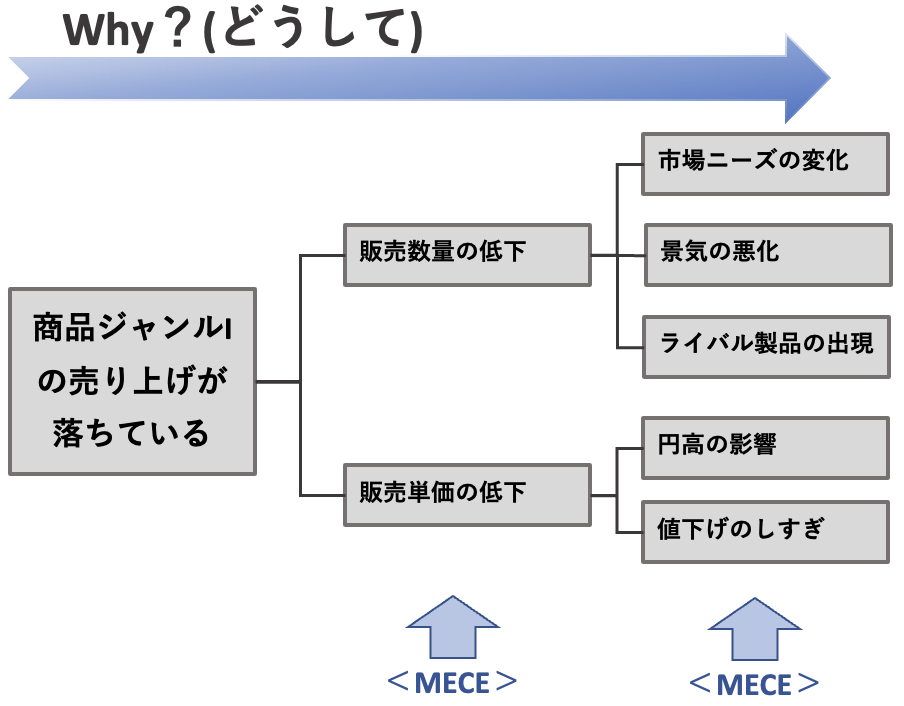
- Howツリー
Howツリーは、解決すべき課題をその具体的な解決策に分解するロジックツリーです。
親要素(左側)の課題の具体的な解決策が子要素(右側)になります。
Howツリーは、解決策の案を網羅的に抽出し、出された解決策の実現性や効果の大小を比較・検討するのに役立ちます。
例えば、「商品ジャンルIの売り上げが落ち込む中で、会社全体の売り上げを維持する」という課題の解決策を網羅的に抽出することで、どの解決策が最も適しているかの比較や検討ができます。
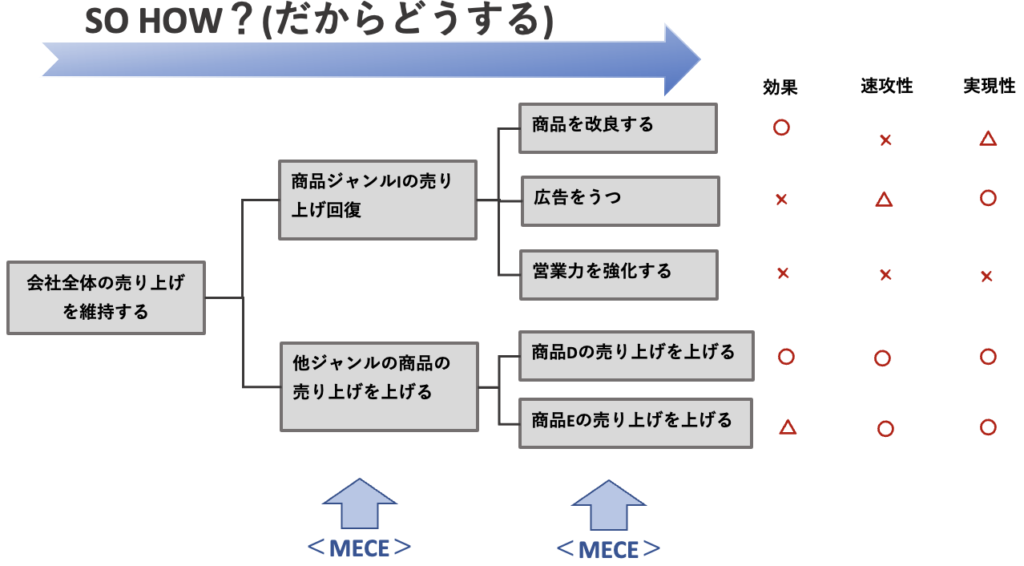
ピラミッドストラクチャー
ピラミッドストラクチャーとは、ある結論や主張とその根拠をピラミッドのように構造的に配置するツールで、ピラミッド構造とも呼ばれます。
親要素(上位)の結論・主張に対して、その結論・主張の根拠が子要素(下位)になります。
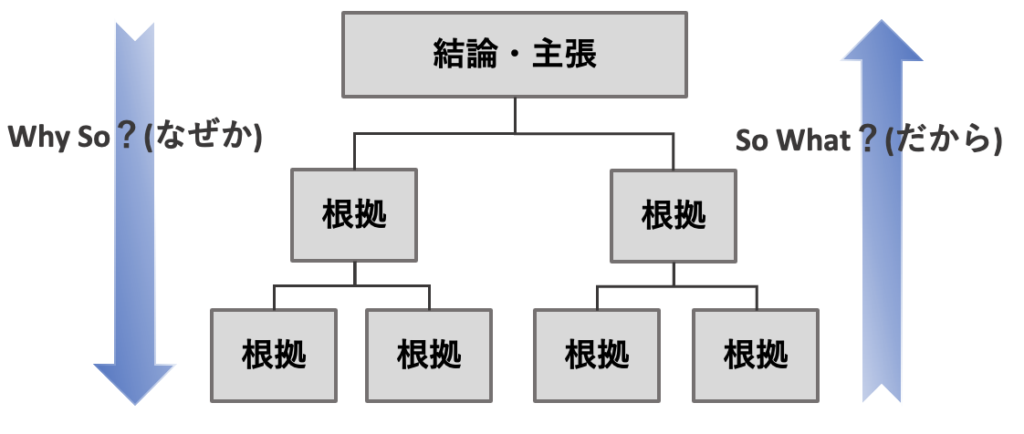
あなたがなぜその結論・主張に至ったのか(Why So)、その根拠は何なのか(So What)というストーリーを説明するときに力を発揮します。
ピラミッドストラクチャで結論とその根拠を整理しておくことで、筋道が通った説明ができるようになります。
また、結論とその根拠との関係を可視化して相手に示すことで、説明を聞いた相手が結論(主張)にいたる論理を理解しやすくなります。
それにより、あなたの説明の説得力が増し、あなたの提案が通りやすくなります。
例えば、今月は商品Cの広告に力を入れるべきという主張とその根拠をピラミッドストラクチャーで示すと、次の図のようになります。
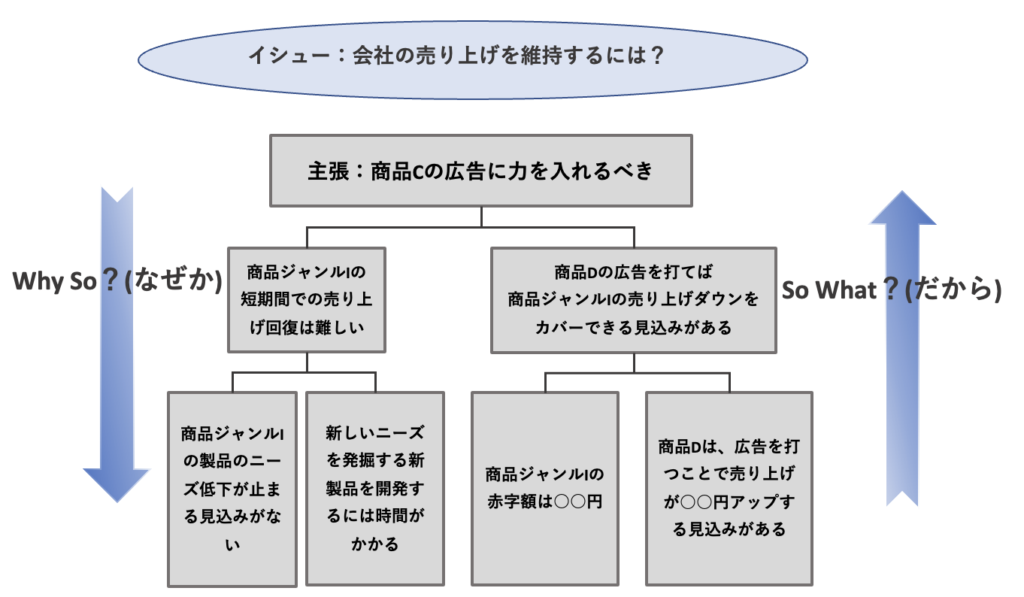
ピラミッドストラクチャーとロジックツリーの違い
ピラミッドストラクチャーとロジックツリーは、形が似ていますがその構造や目的が根本的に違います。
ロジックツリーは左から右に行くにつれて構成要素が分解されて詳細になっていく構造で、問題の原因や解決策を追及する目的で使います。
それに対して、ピラミッドストラクチャーは、結論(主張)とその根拠の関係を示す構造で、結論(主張)に至った経緯を説明したり、その理論の正しさを証明したりする目的で使います。
クリティカルシンキングやラテラルシンキングとの違い

ロジカルシンキングと混同されがちな思考法に、クリティカルシンキングやラテラルシンキングがあります。
ロジカルシンキングとクリティカルシンキングの違い
クリティカルシンキング(批判的思考)とは、問題や課題をどのように解決したら良いかの道筋を定めて、さまざまな角度から論理的に検討していく思考法です。
本当にその道筋で問題ないかを内省しながら、進むべき方向を定めていく思考法であることから批判的思考(クリティカルシンキング)という名がつけられました。
問題解決という点ではロジカルシンキングと共通であり、MECEや演澤法・帰納法など、ロジカルシンキングと重複する手法を使います。
ロジカルシンキングとの違いは、解決すべき問題の抽象度です。
ロジカルシンキングが目に見える具体的な問題の解決に適しているのに対して、クリティカルシンキングでは「どのような手順で検討を進めるか」「どのような意思決定ツールを使うか」といった思考の道筋までを含めて考えるため、より抽象的な問題を解決するのに適しています。
ロジカルシンキングとラテラルシンキングの違い
ラテラルシンキング(水平思考)とは、既存の概念や理論にとらわれないで、自由な発想を連鎖的に展開することで、物事を多面的かつ柔軟に捉え、新しい発想や方式を生み出すための思考法です。
マルタ島の医師、心理学者でありコンサルタントでもあったエドワード・デ・ボノが、従来の論理的思考を垂直思考(バーチカルシンキング)とし、それに対応する思考を水平思考(ラテラルシンキング)として紹介したことから広がりました。
ロジカルシンキングとの違いは、解決すべき問題の新規性です。
ロジカルシンキングが既存のビジネスの問題を解決するのに適しているのに対し、ラテラルシンキングは既存の理論にとらわれない発想を展開することから、誰も経験がないような新しいビジネスに取り組む際のアイデア出しに適しています。
それぞれの思考法の違いのまとめ
ロジカルシンキング、クリティカルシンキング、ラテラルシンキングそれぞれの概念や適切な用途の違いをまとめると、つぎのようになります。
| 思考法 | 概念 | 適切な用途 |
|---|---|---|
| ロジカルシンキング | ツールを用いて物事を分解し分析することで、問題の原因や解決策を導く思考法 | 具体的な問題の解決 |
| クリティカルシンキング | 思考の手順やツールといった問題解決のための道筋まで含めて検討する思考法 | 抽象的な問題の解決 |
| ラテラルシンキング | 既存の概念や理論にとらわれずにアイデアを出す思考法 | 新しい未知の問題の解決 |
ロジカルシンキングの鍛え方

ロジカルシンキングで物事を分析する能力を鍛えるには、これらを日常的に実践するのが有効です。
結論から話す
まず結論を話し、その後に結論に至った根拠や具体例の説明を補足することで、ロジカルシンキングで考える能力が鍛えられます。
最初のうちは、ピラミッドストラクチャーを実際に書いて、それに沿って話をすると良いでしょう。
慣れてくると頭の中でピラミッドストラクチャーを構築して、話ができるようになります。
仮説を立てる
問題や課題に直面したときは、常に仮説を立ててからその分析に取り組むことで、仮説を立てる能力が鍛えられ、より精度が高い仮説を立てられるようになります。
仮説の精度が上がれば、ロジックツリーで課題を分解するときに適切な切り口を選択できるようになるため、ロジカルシンキングで問題解決する能力が高まります。
MECEを意識する
物事を考えるときは常にMECE(モレなくダブりなく)を意識しましょう。
MECEは、ロジカルシンキングの基本中の基本の考え方です。
日頃からMECEで物事を考える癖をつけることで、ロジカルシンキングで問題解決に取り組むときにも自然にMECEで問題を分析できるようになります。
フェルミ推定の問題を解く
フェルミ推定の問題を解くこともロジカルシンキングのトレーニングに有効です。
フェルミ推定とは、実際に調査することが困難な数量を推理し、短時間で計算して答えを導き出すことです。
フェルミ推定の問題を解くには、MECEで考えることや仮説を立てることが必要です。また、帰納法や演澤法を使って推理したり、ロジックツリーやピラミッドストラクチャーを使って思考を整理したりできるため、ロジカルシンキングのトレーニングになります。
例えば、フェルミ推定の有名な問題の一つに「東京都内にあるマンホールの総数はいくつか」という問いがあります。
この問いへの結論を、ピラミッドストラクチャーを使って整理すると次のようになります。
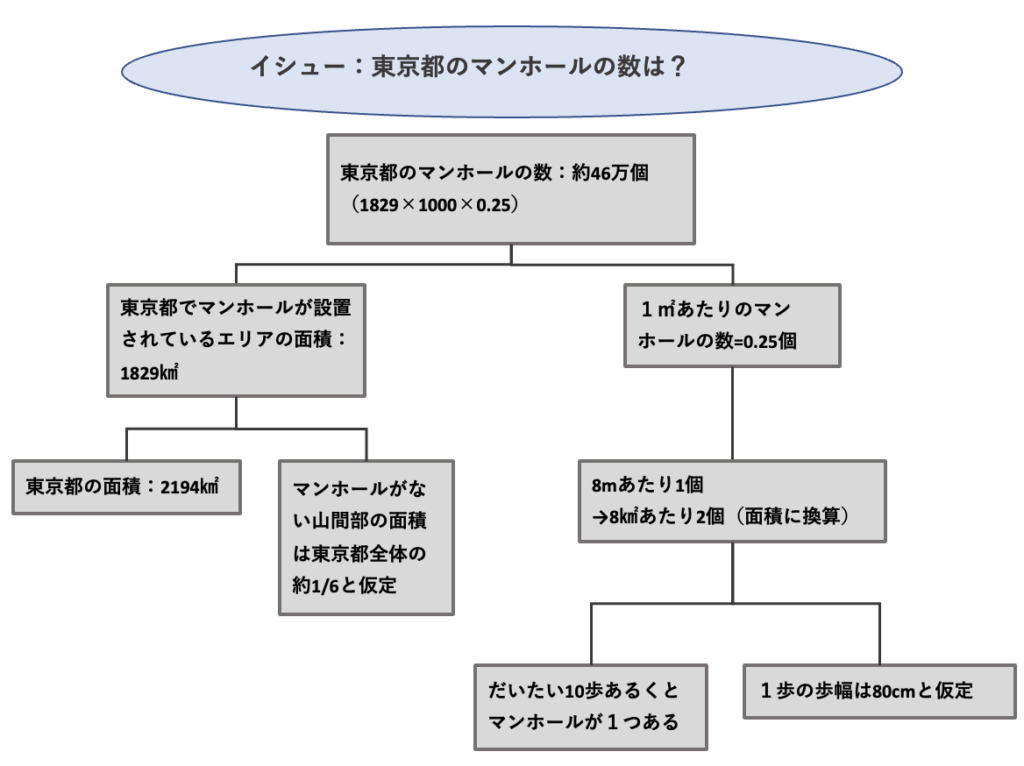
もっと深く学びたい人へ

ロジカルシンキングをもっと深く学びたいと思ったら、書籍や研修で学ぶのがオススメです。
ロジカルシンキングの関連本は多数出版されており、演習問題がついている本もあります。
1冊購入して手元に置いておくとよいでしょう。
また、ロジカルシンキングを教える研修も多数開催されており、検索すればあなたに適した研修がきっと見つかります。
基本は有料になりますが、研修はグループで学習できたり、疑問点をその場で講師に質問できたりするため、ロジカルシンキングをより深く学ぶには最適です。
おすすめの書籍
ロジカル・シンキング 論理的な思考と構成のスキル
日本にロジカルシンキングを広めるきっかけとなった本です。
刊行が2001年と古いですが、初心者が体系的にロジカルシンキングの考え方や基本スキルを学ぶには最適です。
新版 問題解決プロフェッショナル 思考と技術
MECEやロジックツリーを用いた問題解決の実践的な手法が学べる本です。
そのほか仮説思考やゼロベース思考といった、ロジカルシンキングで問題解決する上で欠かせない思考法も学べます。
新版 考える技術・書く技術 問題解決力を伸ばすピラミッド原則
ピラミッドストラクチャーについて詳細に解説されています。
翻訳に難があり、わかりにくい部分もありますが、ピラミッドストラクチャーについて体系的に深く学びたい人にはオススメです。
まとめ

ロジカルシンキングは仕事のあらゆる場面で役に立つ、ビジネスパーソンに必須の思考法です。
問題解決、プレゼンテーション、上司への報告の際などに、MECEで考え、帰納法・演澤法で論理を構築し、ロジックツリーやピラミッドストラクチャーで整理する。
それだけで、あなたの仕事の質やスピードが劇的に高まり生産性が向上します。
ロジカルシンキングを活用して、より高い成果を出せるようになりましょう。






